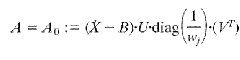| Daniel Anguita | 2273081-9 |
| Marcos Fuentes F. | 2273011-8 |
| Sergio E. Labbé S. | 2273031-2 |
| Francisco J. Riveros E. | 2273036-3 |
| Marcelo Salazar | 2273045-2 |
Lunes 3 de Julio de 2006
1 Resumen
La descomposición en valores singulares (SVD) es utilizada en diferentes áreas de la biología actualmente. En general, SVD se utiliza para el análisis de conjuntos de datos, que a menudo son grandes y “ruidosos”.
Entre las numerosas aplicaciones de SVD en la biología, se destacan en este trabajo tres: Dinámica de proteínas, Análisis de micro-arreglos de datos e Ingeniería inversa en redes genéticas. En cuanto a la dinámica de proteínas, se utiliza la SVD para analizar el movimiento de la hemoglobina muscular (myoglobin) respecto de la dinamica molecular. Según este método sirve para descomponer una trayectoria dinámica molecular hacia dentro de los modos fundamentales del movimiento atómico.
El análisis de micro-arreglos (microarrays) de datos, sirve para comparar distintos micro-arreglos de ADN. Se utiliza SVD en este campo, con el fin de obtener los “genes propios” (eigengenes o filas de la matriz V de la SVD) y el “análisis propio” (eigenassays o columnas de la matriz U de la SVD). Así, se comparan las muestras a través de estos dos parámetros obtenidos de la SVD, de donde se extraen patrones. El objetivo de encontrar estos patrones es lograr clasificar genes, inferir las funciones de los genes. Además, se busca clasificar enfermedades comparando con un micro-arreglo normal y estudiar los efectos de un estímulo interno.
La SVD, también es útil en la ingeniería inversa a redes de genes. La idea, es utilizar SVD para encontrar los mínimos cuadrado para encontrar la expresión que permita localizar una familia de soluciones, es decir, de tomar una matriz que representa genes y experimentos, y a través de mínimos cuadrados, encontrar la mejor familia de soluciones posibles.
Por otro lado, en este trabajo se agregan otros experimentos en los que se usan para analizar las capacidades metabólicas de dos especies de bacterias, comprobándose en estas dos que el “helicobacter pylori” tiene una red metabólica mas rígida que la “Haemophilus influenzae” para la producción de aminoácidos; Siendo la SVD, capaz de identificar los principales puntos de control para la regulación. Luego como punto principal del uso de SVD, fue que gracias a este procedimiento, se pudo aplicar a grandes números de ejemplos, por lo que se ocupan en grandes redes de genoma, antes difíciles de aplicar sin una transformación.
2 Introducción
La descomposición en valores singulares (SVD), es una herramienta en el álgebra lineal muy potente, que es muy usada para diversos ámbitos de investigación tanto como para análisis sintácticos como para la biología, entre otros casos. La SVD permite, a través de una serie de operaciones lineales elementales (todas las que involucran suma y/o multiplicación de filas y/o columnas), descomponer la información contenida en la matriz de datos y representar, en otras tres matrices, aspectos singulares o característicos de aquella información.
El principio de descomposición involucra la reducción del elevado numero de dimensiones con que los datos son descritos en la primera matriz, las que impiden distinguir los valores singulares. La reducción, en tanto, consiste en desechar la información incidental (es datos irrelevantes) considerado como ruido en los datos, proporcionando así un modelo de distribución normalizado de las frecuencias o modelo sin ruido, el que redunda en una representación matemática mas compacta y, por tanto, mas simple de computar.
Las matrices resultantes de la operación son:
- Matriz ortogonal (U en la Figura 1): obtenida al procesar linealmente el número de columnas (ortogonal) de la matriz original (A en el ejemplo de la Figura 1). En esta matriz se representan datos como vectores en espacios de datos.
Figura 1 : Representación de matriz ortogonal
b) Matriz transpuesta (V en la Figura 2): obtenida al permutar las filas por las columnas), proporcionando una disposición ortogonal de los elementos de la fila A través de esta transposición se presentan documentos como vectores en espacios de datos.

Figura 2 : Representación de matriz transpuesta.
c) Matriz diagonal (E en la Figura 3): obtenida al procesar linealmente el número de filas, el número de columnas y la cantidad de dimensiones de la matriz original (A). La matriz diagonal representa el valor singular de (A) y en ella todos los elementos que no pertenecen a la diagonal son nulos o iguales a cero.
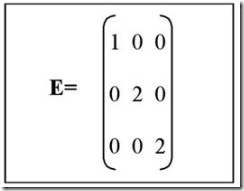
Figura 3 : Representación de matriz diagonal.
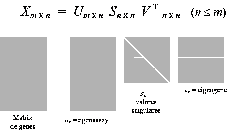
Las tres nuevas matrices (U), (V) y (E) dan origen a los vectores singulares de la representación matricial del corpus (A), a saber, vector de palabras, de documentos y de valor singular, respectivamente .La Figura 4, que se presenta a continuación, grafica la factorización con SVD.
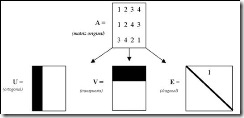
Figura 4 : Representación de SVD
Si las tres nuevas matrices fueran multiplicadas, el producto resultante sería semejante, pero nunca idéntico a la matriz original, pues las dimensiones de esta ya han sido reducidas y solo puede ser reconstituida la información esencial, producto definido como valor singular (matriz E) y vectores singulares (matrices U y V). De este modo, tras la SVD se obtiene una información que no está directamente disponible en la primera representación matricial, sino que está latente en ella .
3 Tema de Aplicación
3.1 Dinámica de Proteínas
Como dijimos anteriormente en la introducción, por medio del análisis del SVD se ha usado para caracterizar a las proteínas dinámicas. En este caso se usa una SVD para analizar el movimiento de la hemoglobina muscular (myoglobin).Ya que según el profesor Romo [[1]], usando los métodos de dinámica molecular, es posible medir las posiciones atómicas de todos los átomos muestreados durante una simulación.
En el método de dinámica molecular se trabaja de la siguiente forma en un software:
Se leen los parámetros que especifican las condiciones de la corrida tales como la temperatura inicial, el numero de partículas, la posición de las partículas (estructura fcc, bcc, etc.) la densidad, el paso de tiempo Δt, tiempo total de simulación, etc.
Se inicializa el sistema, esto es, se asignan las posiciones y las velocidades iniciales.
Se calculan las fuerzas sobre todas las partículas.
Se integran las ecuaciones de movimiento de Newton. Este paso así como el anterior conforman el loop central de la simulación. Ellos son repetidos hasta haber calculado la evolución temporal del sistema durante el tiempo total de simulación deseado. Se van guardando las posiciones, velocidades, fuerzas, etc., durante cada paso en un archivo para luego ser procesadas.
Después de haber completado lo anterior, se calculan y se imprimen los diferentes promedios relevantes.
En otros experimentos el Prof. Ozkan, uso la SVD para el estudio si dos-estados proteínicos se pliegan en caminos o canales (funnels). El plegamiento proteico, es la segunda traducción del mensaje genético, este completa la información transferida del DNA al producto final, la proteína activa. En otras palabras, para entender completamente este proceso, es necesario descifrar el código de plegamiento, la segunda parte del mensaje genético:
DNA → RNA → cadena polipeptídica → ¿Proceso de plegamiento? →Proteina activa
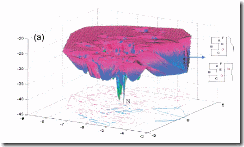
Según el estudio de Ozkan, mostró que el modelo de plegamiento puede producir que esconda intermediarios. Una gran multiplicidad de trayectorias fueron observadas a nivel microscópico, empero estas colapsaban al esconder intermediarios a nivel microscópico corriendo en paralelo. Esta SVD fue usada para procesar estos datos, bajando a un nivel que podría ser analizado visualmente. Una matriz de 32 x M, fue creada fuera de M conformaciones de los 16mer cadenas de aminoácidos. Aquí las eigenfilas de los dos más grandes valores singulares fueron usadas como eje para un grafico 3-dimensional con el eje-z representando a la energía. Así, una representación de dos dimensiones de la energía de vista fue desarrollada usando la SVD. Por ejemplo podemos ver una vista para configuraciones para 4 o más contactos:
3.2 Análisis de Micro-Arreglos de Datos.
Los micro arreglos de datos, se entienden como matrices en las que las filas corresponden a genes, mientras que las columnas son experimentos, por lo que cada entrada de la matriz aij, es la respuesta del gen i cuando se aplica el experimento j. En la siguiente figura se muestra la descomposición.
En este caso, las columnas de la matriz U de la SVD recibe el nombre de “análsis propio”, mientras que las filas de la matriz V “genes propios” (de ahora en adelante se utilizan los nombres en inglés que están en la figura. La idea, es que la respuesta de un gen frente a un estimulo, se puede escribir como combinación lineal del eigengen, mientras que la expresión de un experimento, como combinación lineal de un eigenassay.
Alineando el procedimiento con los fundamentos de la SVD, tenemos que la matriz que contiene los datos experimentales, se descompone en sus vectores propios y en otros que deforman estos vectores. La SVD tradicional, muestra que la matriz de datos en este caso parte de una circunferencia formada por los vectores propios de norma 1, y que se amplifica con la matriz que contiene los valores singulares, para luego rotar el producto de lo anterior y generar una hiper-elipse rotada a partir de la circunferencia de radio 1. La matriz de valores singulares y las columnas de la matriz U de eigenassays, representan los estímulos proporcionados a los genes en estado natural que son representados por las filas de la matriz V.
3.3 Ingeniería Inversa en Redes Genéticas
Si un sistema se encuentra operando cerca de un estado estable, las dinámicas (fluctuaciones de la concentración en una red de genes) se pueden aproximar a través de la ecuación:
Donde x, es la concentración de mRNAs que reflejan los niveles de expresión de los genes, los λi, representan las tasas de auto-degradación, las Wij, describe el tipo y fuerza de la interacción entre los genes i y j, las bi, son el estímulo interno, y εi representan el ruido.
Un experimento aplica un estímulo y usa un micro-arreglo para medir las concentraciones de N mRNAs diferentes. Al repetir M veces este experimento, se puede obtener una estimación de x.
Ahora, la ecuación anterior, puede escribirse en forma matricial, de la siguiente manera:
Donde la matriz A es una combinación de W, es decir, que la solución para A, permite obtener W, que es lo que se busca.
El objetivo de la ingeniería inversa, es usar la matriz medida B, X y X’ para deducir A y por lo tanto la matriz de conectividad W. Tomando la transpuesta del sistema anterior, queda:
Si M = N, y además X es de rango completo, basta con invertir X para encontrar A. Sin embargo, típicamente, M es mucho mayor que N por el alto costo de perturbaciones y medidas. Por lo tanto, se tiene un problema indeterminado. Una forma de abordar el problema es utilizando la SVD, donde al descomponer la transpuesta de X queda:
Si se asume que todos los valores singulares de la transpuesta de X están al final de la diagonal de W, se puede obtener una solución particular para A:
Donde 1/wj se reemplaza por 0 si wj = 0.
Por lo anterior, sabemos que todas las posibles soluciones son:
La solución a elegir, es aquella que los errores de mínimos cuadrados. Este método, trata de encontrar una solución que se acerque lo más posible a la encontrada.
Cabe señalar que las redes de genes a menudo son poco densas, esto quiere decir que la mayoría de los genes no interactúa con otros. Por lo que en vez de buscar una solución con el mínimo error cuadrático, se busca por una solución con el mínimo número de conexiones, o la “matriz de escasez”.
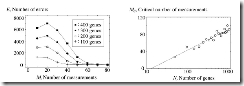
En el gráfico de la izquierda, se muestra el número de errores (E), cometidos por la ingeniería inversa como una función de M, el número de medidas.
El segundo gráfico, muestra el número crítico de medidas, Mc, requerida para cubrir correctamente la matriz de conectividad, en función de N, el tamaño de la red para sistemas lineales. Los círculos muestran los datos , mientras que la recta, es la aproximación por mínimos cuadrados.
3.4 Otros Problemas
Sobre otras aplicaciones de la SVD, podemos ver el uso para analizar las capacidades metabólicas de dos especies de bacterias. El análisis del espacio de soluciones y la dominancia del primer valor singular revelo que la “Helicobacter pylori” tiene una red metabólica mas rígida que la “Haemophilus influenzae” para la producción de aminoácidos. Así la SVD fue capaz de identificar las principales ramas de la red que pueden ser identificados como principales puntos de control para la regulación.
En ese estudio se mostró que la SVD de una matriz (W) formada para un random de ejemplos desde el espacio de soluciones en el estado estacionario de las redes metabólicas hRBC (human red blood cell) dan acercamientos similares dentro de las propiedades regulatorias de la red, tal como fueron obtenidas con la SVD de P, obtenida de los Extreme pathways (ExPas). Estos nuevos acercamientos tienen dos principales ventajas. Primero, esto funciona con una representación directa de las formas del espacio de soluciones metabólicos sin el factor de unión de una distribución no uniforme de los Extreme pathways y segundo, que el procedimiento SVD puede ser aplicado a grandes números de ejemplos, tal como sería producido desde las redes genome-scale.
4 Aporte Grupal
Dinámica de Proteínas.
En este caso, SVD provee de un método para descomponer una trayectoria dinámica molecular hacia dentro de los modos fundamentales del movimiento atómico. Los vectores singulares derechos, son proyecciones de las estructuras de proteínas sobre estos modos fundamentales mostrando el movimiento de la proteína en una base generalizada de bajas dimensiones. En este caso, análisis estadísticos de los vectores singulares derechos, pueden ser usados para clasificar sub-estados configuracionales discretos en la proteína. Luego, el retrato del espacio configuracional formado desde los vectores singulares derechos, pueden también ser usados para visualizar un movimiento complejo de dimensiones altas, y asimismo para examinar la magnitud del espacio muestreado por la simulación.
Análisis de Micro-Arreglos de Datos.
Los micro-arreglos son una de las últimas brechas en la biología molecular, el cual permite el monitoreo de la expresión de genes de miles de millones en paralelo y ya se esta produciendo una gran cantidad de información con estos datos. El análisis y manejo de estos datos se a convertido en uno de los mayores cuellos de botella en la utilización de esta tecnología. El fondo de los micro-arreglos son las imágenes, donde deben ser transformadas a expresiones matriciales de genes, es decir, tablas donde las filas representan genes y las columnas representan varios muestreos como tejidos finos de las condiciones experimentales, y los numeros en cada celda caracterizan a nivel de expresión particular de cada gen en una muestra particular. Estas matrices deben ser analizadas posteriormente, si cualquier conocimiento adyacente a los procesos biológicos es extraído.
Ingeniería Inversa en Redes Genéticas.
Descubriendo y entendiendo la complejidad de la interacción molecular que se traduce en un organismo vivo es uno de los restos más interesante de la biología molecular moderna. Por esto se usa ingeniería inversa optimizada buscando la reconstrucción de red de interacción entre genes dinámicos. La aproximación se basa en los micro-arreglos de datos y los conocimientos de la biología actual. Así se identifican estructuras de redes buscando sistemas ordinarios de ecuaciones diferenciales, las cuales simulan comportamientos que pueden encajar en la expresión de los genes. Métodos de re-muestreo son aplicados para validar el modelo de red dinámica.
Este algoritmo fue aplicado para diferenciar los distintos micro-arreglos de DNA.
5 Conclusiones
No cabe la menor duda que la técnica SVD, junto al gran avance computacional, se esta transformando en algo esencial y relevante para la biología, debido a que entrega la información de un punto de vista factorizado, sino que también esta filtra información redundante que muchas veces no hacen mas que entorpecer la etapa de análisis. La importancia de la SVD en biología puede ser apreciada si se revisan papers relacionados con el tema, de los cuales 81 realizan una referencia a esta técnica desde el año 2002, donde se mencionan nuevas técnicas y usos de esta descomposición de datos. Como los biólogos se han adaptado mejor a nuevas técnicas y herramientas, el uso de la SVD continuará creciendo en un futuro cercano.
[1] Romo T.D., Clarage J.B., Sorensen D.C., Phillips G.N., Jr. Automatic identification of
discrete substates in proteins: singular value decomposition analysis of timeaveraged
crystallographic refinements. Proteins 1995; 22:311-21.